数据结构概述、线性结构

发表于 阅读次数：
本文字数： 14k 阅读时长 ≈ 13 分钟

像你

数据结构与算法基础

概述

数据结构概述

数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成

数据的存储结构

  • 顺序存储结构

把数据元素存放在地址连续的存储单元里、其数据间的逻辑关系和物理关系是一致的、数组就是顺序存储结构的典型代表

顺序存储结构

  • 链式存储结构

把数据元素存放在内存中的任意存储单元里、也就是可以把数据存放在内存的各个位置、这些数据在内存中的地址可以是连续的、也可以是不连续的

链式存储结构

数据的逻辑结构

  • 集合结构

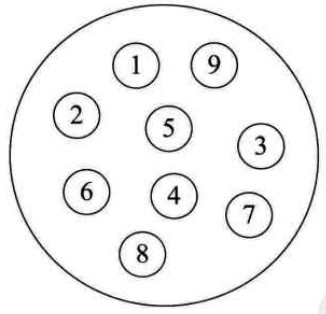
集合结构中的数据元素同属于一个集合、他们之间是并列的关系、除此之外没有其他关系

集合结构

  • 线性结构

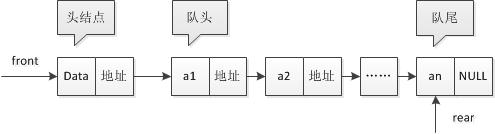
线性结构中的元素存在一对一的相互关系

线性结构

  • 树形结构

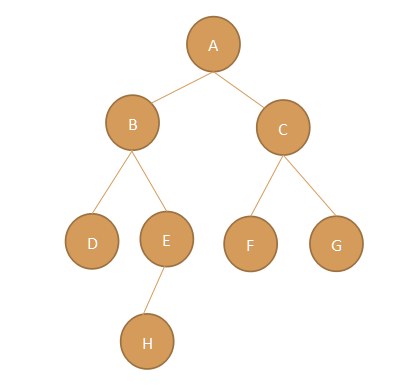
树形结构中的元素存在一对多的相互关系

树形结构

  • 图形结构

图形结构中的元素存在多对多的相互关系

图形结构

算法概述

是指解题方案的准确而完整的描述、是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制

算法的特性

  • 输入
  • 输出
  • 有穷性
  • 确定性
  • 可行性

算法的基本要求

  • 正确性
  • 可读性
  • 健壮性
  • 时间复杂度
  • 空间复杂度

线性结构

数组

数组

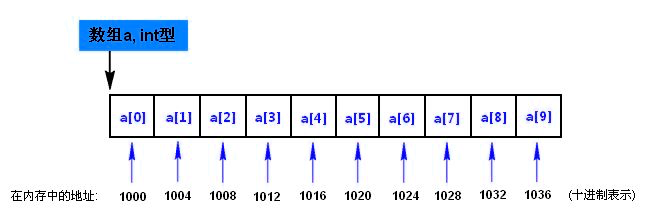
数组的基本使用

  • 添加数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class AddData {

    //给数组中添加数据
    public static void main(String[] args) {

        //创建数组
        int [] arr = new int[] {5,2,1};

        //输出arr数组数据
        System.out.println(Arrays.toString(arr));

        //定义要添加的数据
        int number = 0;

        //创建新数组长度为arr数组+1
        int [] newArr = new int[arr.length + 1];

        //将数据添加到新数组末端
        newArr[arr.length] = number;

        //将原数组数据复制给新数组
        for(int i = 0; i < arr.length; i++){
            newArr[i] = arr[i];
        }

        //新数组替换原数组
        arr = newArr;

        //输出更新后数组
        System.out.println(Arrays.toString(arr));
    }
}
  • 删除数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public class DeleteData {

    public static void main(String[] args) {

        //创建一个数组长度为6、含有12个元素
        int [] arr = new int[]{9,8,7,6,5,4,2,1,4,5,6,7};

        //输出原数组
        System.out.println(Arrays.toString(arr));
        //创建一个新数组
        int [] newArr = new int[arr.length - 1];

        //生成一个随机数、用于代表要删除的位置
        int number = (int) (Math.random() * 10);

        //输出删除下标
        System.out.println(number);

        //删除替换
        for(int i = 0; i < number; i++){
            newArr[i] = arr[i];
        }
        for(int i = number+1; i < arr.length; i++){
            newArr[i - 1] = arr[i];
        }

        //新数组替换源数组
        arr = newArr;

        //输出原数组
        System.out.println(Arrays.toString(arr));
    }
}

查找算法

  • 线性查找

线性查找就是从数组头部开始、依次向后查找、一直到查到结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//线性查找
public class Wire {

    public static void main(String[] args) {

        //声明一个数组
        int[] elements = new int[]{1,6,5,43,1,56,4,1,4,1,54,2,43};

        //创建一个默认下标、默认为-1
        int index = -1;

        //声明一个要查找的元素
        int target = 5;

        //遍历数组、从头开始查看是否有与target相等的
        for(int i = 0; i < elements.length; i++ ){
            if(elements[i] == target){
                index = i;
                break;
            }
        }
        System.out.println("index = " + index);
    }
}
  • 二分法查找

首先二分法查找的数组必须为有序的、然后取数组中间位置查看、查看此刻的值与要查询的值的关系、如果相对较小则取较小的一边、然后再次取中间位置查看、再次进行比较、依此类推此法、相对较大则同理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
//二分法查找
public class Dichotomy {

    public static void main(String[] args) {

        //定义一个数组
        int[] arr = new int[]{1,2,3,4,5,6,7,8,9};

        //目标位置
        int index = -1;

        //定义一个要查询的值
        int target = 5;

        //起始位置
        int begin = 0;

        //末位置
        int end = arr.length - 1;

        //中间位置
        int mid = (begin + end) / 2;

        //开始循环
        while (true){
            //中间值是否与查询的相等
            if(arr[mid] == target){
                index = mid;
                break;
            }else{
                //查询内容比中间值小时
                if(target < arr[mid]){
                    //将末位置改成中间位置前一个
                    end = mid - 1;
                }else{
                    //将起始位置改为中间位置后一个
                    begin = mid + 1;
                }
                //重新取中间值
                mid = (begin + end) / 2;
            }
        }
        System.out.println("index = "  + index);
    }
}

面向对象的数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
public class MyArrays {

    //定义一个数组
    private int[] elements;

    //初始化数组
    public MyArrays(){
        this.elements = new int[0];
    }

    /**
     * 插入数据
     * @param element
     */
    public void add(int element){
        //创建一个新的数组、长度为原数组+1
        int[] newArr = new int[elements.length + 1];

        //添加数据
        for(int i = 0; i <elements.length; i++){
            newArr[i] = elements[i];
        }
        newArr[elements.length] = element;

        //更新原数组
        this.elements = newArr;
    }

    /**
     * 插入到指定位置元素
     * @param index
     * @param element
     */
    public void add(int index,int element){

        int[] newArr = new int[elements.length + 1];

        for (int i = 0; i < elements.length; i++){
            if(i < index){
                newArr[i] = elements[i];
            } else{
                newArr[i+1] = elements[i];
            }
        }
        newArr[index] = element;

        this.elements = newArr;
    }

    /**
     * 删除数据
     * @param index
     */
    public void delete(int index){

        int[] newArr = new int[elements.length - 1];

        for(int i = 0; i < newArr.length; i++){
            if(i < index){
                newArr[i] = elements[i];
            }else{
                newArr[i] = elements[i+1];
            }
        }
        this.elements = newArr;
    }

    /**
     * 更新数据
     * @param index
     * @param element
     */
    public void update(int index, int element){

        if(index < 0 || index > elements.length - 1){
            throw new RuntimeException("数组下标越界");
        }

        this.elements[index] = element;
    }

    //根据下标取出数据
    public int get(int index){

        if(index < 0 || index > elements.length - 1){
            throw new RuntimeException("数组下标越界");
        }
        return elements[index];
    }

    //数组长度
    public int size(){

        return elements.length;
    }

    //输出数组元素
    public void show(){
        System.out.println(Arrays.toString(this.elements));
    }


    /**
     * 线性查询
     * @param target
     * @return
     */
    public int wire(int target){

        //遍历数组、从头开始查看是否有与target相等的
        for(int i = 0; i < elements.length; i++ ){
            if(elements[i] == target){
                return i;
            }
        }
        return -1;
    }

    /**
     * 二分法查询
     * @param target
     * @return
     */
    public int dichotomy(int target){

        //起始位置
        int begin = 0;

        //末位置
        int end = elements.length - 1;

        //中间位置
        int mid = (begin + end) / 2;

        //开始循环
        while (true){

            //当起始位置大于等于末位置时说明数组中没有查询的内容
            if(begin >= end){
                return -1;
            }

            //中间值是否与查询的相等
            if(elements[mid] == target){
                return mid;
            }else{
                //查询内容比中间值小时
                if(target < elements[mid]){
                    //将末位置改成中间位置前一个
                    end = mid - 1;
                }else{
                    //将起始位置改为中间位置后一个
                    begin = mid + 1;
                }
                //重新取中间值
                mid = (begin + end) / 2;
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public class Test {

    public static void main(String[] args) {
        MyArrays arrays = new MyArrays();

        //添加
        arrays.add(1);
        arrays.add(2);
        arrays.add(3);
        arrays.add(4);
        arrays.add(5);
        arrays.add(6);
        arrays.add(7);
        arrays.add(8);
        arrays.add(9);

        //线性查找
        System.out.println(arrays.wire(4));
        //二分法查找
        System.out.println(arrays.dichotomy(0));

        //在指定位置添加
        arrays.add(2,5);
        arrays.show();
        System.out.println("----------------");

        //删除
        arrays.delete(1);
        arrays.show();
        System.out.println("----------------");

        //数组长度
        System.out.println("数组的长度为：" + arrays.size());
        System.out.println("----------------");

        //根据下标查询内容
        System.out.println(arrays.get(2));
        System.out.println("----------------");

        //更新数据
        arrays.update(2,100);
        arrays.show();
    }
}

栈

栈的数据特点是顺序结构、先进后出

栈结构

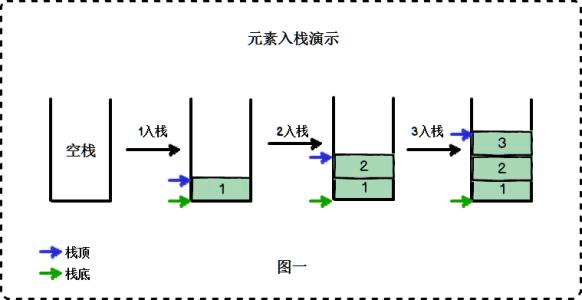
简单示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
public class MyStack {

    //定义栈结构
    private int[] elements;

    //初始化栈
    public MyStack(){
        this.elements = new int[0];
    }

    /**
     * 添加数据到栈中
     * @param element
     */
    public void push(int element){
        //创建一个新的数组、长度为原数组+1
        int[] newArr = new int[elements.length + 1];

        //添加数据
        for(int i = 0; i <elements.length; i++){
            newArr[i] = elements[i];
        }
        newArr[elements.length] = element;

        //更新原数组
        this.elements = newArr;
    }

    /**
     * 取出栈顶的数据
     * @return
     */
    public int pop(){

        //栈是空的时候有个异常
        if(elements.length == 0){
            throw new RuntimeException("栈是空的");
        }

        //取出最后一个放入栈中的元素
        int element = this.elements[elements.length - 1];

        //创建取出后的栈结构数组
        int[] newArr = new int[elements.length - 1];

        //将源数据放入到新数组中
        for(int i = 0; i < elements.length - 1; i++){
            newArr[i] = this.elements[i];
        }

        //更新栈结构
        this.elements = newArr;

        //返回栈顶的值
        return element;
    }

    /**
     * 查询栈顶元素
     * @return
     */
    public int peek(){
        if(elements.length == 0){
            throw  new RuntimeException("栈是空的");
        }
        return this.elements[elements.length - 1];
    }

    /**
     * 判断栈是否为空
     * @return
     */
    public String isEmpty(){

        return this.elements.length == 0?"栈是空的":"栈不是空的";
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class testStack {

    public static void main(String[] args) {
        MyStack myStack = new MyStack();

        myStack.push(9);
        myStack.push(8);
        myStack.push(7);
        myStack.push(6);

        System.out.println(myStack.isEmpty());
        System.out.println(myStack.pop());
        System.out.println(myStack.pop());
        System.out.println(myStack.pop());
        System.out.println(myStack.pop());
        System.out.println(myStack.isEmpty());
        System.out.println(myStack.peek());
    }
}

队列

队列的数据特点是顺序结构、先进先出

结构

样式

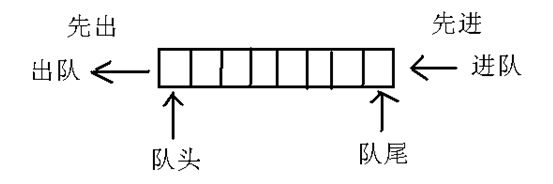
简单示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
public class MyQueue {

    //定义一个数组
    private int[] elements;

    //初始化
    public MyQueue(){
        this.elements = new int[0];
    }

    /**
     * 入队
     * @param element
     */
    public void add(int element){
        //创建一个新的数组、长度为原数组+1
        int[] newArr = new int[elements.length + 1];

        //添加数据
        for(int i = 0; i <elements.length; i++){
            newArr[i] = elements[i];
        }
        newArr[elements.length] = element;

        //更新原数组
        this.elements = newArr;
    }

    /**
     * 出队
     * @return
     */
    public int poll(){

//        出队
        int element = this.elements[0];

//        创建新数组
        int[] newArr = new int[elements.length - 1];

//        将数据赋值到新数组
        for(int i = 0; i < newArr.length; i++){
            newArr[i] = elements[i +1];
        }

//        数据更新
        this.elements = newArr;

//        返回出队数据
        return element;
    }

    /**
     * 队列是否为空
     * @return
     */
    public String isEmpty(){

        return this.elements.length == 0?"队列为空":"队列不为空";
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class TestQueue {

    public static void main(String[] args) {
        MyQueue mq = new MyQueue();

//        入队
        mq.add(5);
        mq.add(2);
        mq.add(0);

//        判断是否为空
        System.out.println(mq.isEmpty());
//        出队
        System.out.println(mq.poll());
//        入队
        mq.add(6);
//        出队
        System.out.println(mq.poll());
        mq.add(7);
        System.out.println(mq.poll());
        mq.add(8);
        System.out.println(mq.poll());
        System.out.println(mq.poll());
        System.out.println(mq.poll());
        System.out.println(mq.isEmpty());
    }
}

单链表

单链表的数据结构是链表的形式存储的、当存储数据的同时要存储下一个结点的地址

单链表

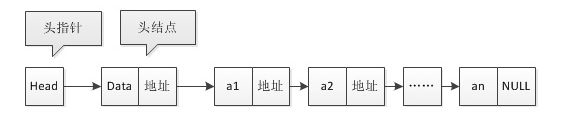
简单示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
public class MyNode {

    //结点内容
    private int data;

    //下一节点
    private MyNode next;

    //初始化
    public MyNode(int data){
        this.data = data;
    }

    /**
     * 追加
     * @param node
     * @return
     */
    public MyNode append(MyNode node){

        //定义当前节点
        MyNode currentNode = this;

        while(true){

            //取出下一节点
            MyNode nextNode = currentNode.next;

            //判断取出的下一个节点是否为空
            if(null == nextNode){
                break;
            }
            //将取出的下一节点赋值给当前节点
            currentNode = nextNode;
        }
        //追加为当前节点的下一节点
        currentNode.next = node;

        return this;
    }

    /**
     * 取出数据
     * @return
     */
    public int getData(){
        return this.data;
    }

    /**
     * 下一节点
     * @return
     */
    public MyNode next(){
        return this.next;
    }

    /**
     * 判断下一节点是否为空
     * @return
     */
    public String islast(){
        return this.next == null?"下一个结点为空":"下一节点不为空";
    }

    /**
     * 删除节点、删除原理是将当前节点的下一节点删除、将下下节点连接到当前节点的下一节点
     */
    public void deleteNode(){

        //下下节点
        MyNode newNode = this.next.next;

        //将下下节点连接到当前节点的下一节点
        this.next = newNode;
    }


    /**
     * 在指定位置添加
     * @param node
     */
    public void insert(MyNode node){

        //取到下个节点
        MyNode nextNext = this.next;

        //将添加的内容添加到下一节点的开始
        this.next = node;

        //将下个节点的内容添加到新加入的节点后面
        node.next = nextNext;
    }

    /**
     * 显示全部节点信息
     */
    public void show(){

        //当前节点
        MyNode currentNode = this;

        while(true){
            //当前节点内容
            System.out.print(currentNode.data + "  ");

            //当前节点的下一节点
            currentNode = currentNode.next;

            //下一节点是否为空
            if(currentNode == null){
                break;
            }
        }
        System.out.println();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class TestNode {

    public static void main(String[] args) {

        MyNode node1 = new MyNode(1);
        MyNode node2 = new MyNode(2);
        MyNode node3 = new MyNode(3);
        MyNode node4 = new MyNode(4);
//        System.out.println(node1.islast());
        node1.append(node2).append(node3).append(node4);
//        System.out.println(node1.islast());
//
//        System.out.println(node1.next().next().next().getData());

        node1.show();

//        node1.next().next().deleteNode();

        node1.next().insert(new MyNode(9));

        node1.show();
    }
}

循环链表

循环链表就是最后一位的下一节点是起始位

循环链表

简单示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class LoopNode {

    //结点内容
    private int data;

    //下一节点
    private LoopNode next = this;

    //初始化
    public LoopNode(int data){
        this.data = data;
    }


    /**
     * 取出数据
     * @return
     */
    public int getData(){
        return this.data;
    }

    /**
     * 下一节点
     * @return
     */
    public LoopNode next(){
        return this.next;
    }

    /**
     * 删除节点、删除原理是将当前节点的下一节点删除、将下下节点连接到当前节点的下一节点
     */
    public void deleteNode(){

        //下下节点
        LoopNode newNode = this.next.next;

        //将下下节点连接到当前节点的下一节点
        this.next = newNode;
    }

    /**
     * 在指定位置添加
     * @param node
     */
    public void insert(LoopNode node){

        //取到下个节点
        LoopNode nextNext = this.next;

        //将添加的内容添加到下一节点的开始
        this.next = node;

        //将下个节点的内容添加到新加入的节点后面
        node.next = nextNext;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static void main(String[] args) {
        LoopNode loopNode1 = new LoopNode(1);
        LoopNode loopNode2 = new LoopNode(2);
        LoopNode loopNode3 = new LoopNode(3);
        LoopNode loopNode4 = new LoopNode(4);

        loopNode1.insert(loopNode2);
        loopNode2.insert(loopNode3);
        loopNode3.insert(loopNode4);
        System.out.println(loopNode1.next().getData());
        System.out.println(loopNode2.next().getData());
        System.out.println(loopNode3.next().getData());
        System.out.println(loopNode4.next().getData());
    }

双链表

双链表的数据结构是存储两个节点、一个存储上一个节点、一个存储下一个节点、因为双链表是循环的所以没有最后一个节点

双链表

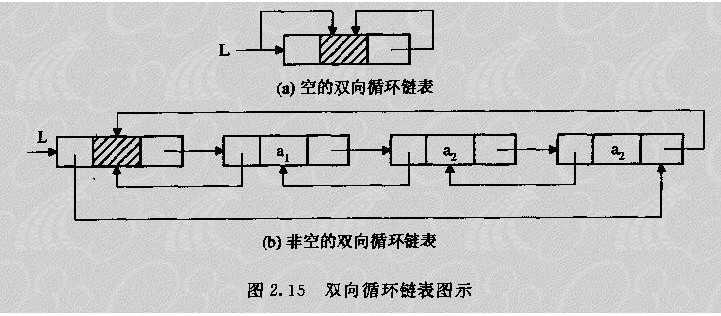
简单示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
public class DoubleNode {

//    上一个结点
    private DoubleNode pre = this;

//    下一个结点
    private DoubleNode next = this;

//    结点内容
    private int data;

//    初始化数据
    public DoubleNode(int data){
        this.data = data;
    }

//    获取上一节点
    public DoubleNode getPre(){
        return this.pre;
    }

//    获取下一节点
    public DoubleNode getNext(){
        return this.next;
    }

//    获取数据内容
    public int getData(){
        return this.data;
    }

    public void inser(DoubleNode node){

//        原结点的下一节点
        DoubleNode nextNext = this.next;

//        将插入的节点连接到源节点上面
        this.next = node;

//        插入的节点的上一节点是源节点
        node.pre = this;

//        插入的节点的下一节点是原结点的下一节点
        node.next = nextNext;

//        源节点的下一节点的上一节点连接到插入的节点上面
        nextNext.pre = node;

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class TestDoubleNode {

    public static void main(String[] args) {

//        创建节点
        DoubleNode node1 = new DoubleNode(1);
        DoubleNode node2 = new DoubleNode(2);
        DoubleNode node3 = new DoubleNode(3);

//        追加节点
        node1.inser(node2);
        node2.inser(node3);

//        查看node2的上一个节点内容、自己的内容、下一节点的内容
        System.out.println(node2.getPre().getData());
        System.out.println(node2.getData());
        System.out.println(node2.getNext().getData());
    }
}

递归

在一个方法（函数）的内部调用该方法（函数）本身、并且有一个条件能使它停止调用自己本身 的编程方式

递归

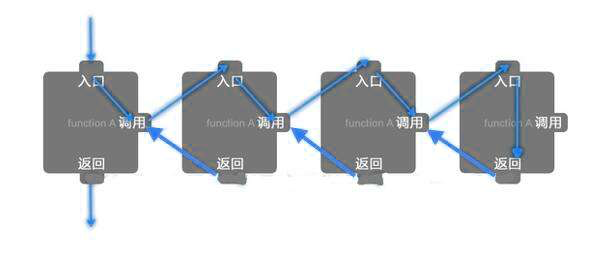
简单示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class TestRecursion {

    public static void main(String[] args) {

        printf(10);
    }

    public static void printf(int i){

        if(i >0){
            System.out.println(i);
            printf(i - 1);
        }
    }
}

斐波那契数列

第一位为1、第二位为1、其余后面的都为 前两位相加的和
1、1、2、3、5、8 ……

  • 显示前10位的斐波那契数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class FBNQ {

    public static void main(String[] args) {

        int i = 10;
        while (i > 0){
            System.out.println(printf(i));
            i--;
        }
    }

    public static int printf(int i){
        if((i == 1) || (i == 2)){
            return 1;
        }else{
            return printf(i - 2) + printf(i - 1);
        }
    }
}

正确的开始、微小的长进、然后持续、嘿、我是小博、带你一起看我目之所及的世界……

-------------本文结束 感谢您的阅读-------------

本文标题:数据结构概述、线性结构

文章作者:小博

发布时间:2021年08月02日 - 11:01

最后更新:2021年08月02日 - 11:19

原始链接:https://codexiaobo.github.io/posts/675515198/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。