
树结构
树结构概述
啥是树结构
树是一种重要的非线性数据结构,直观地看,它是数据元素(在树中称为结点)按分支关系组织起来的结构,很象自然界中的树那样
为什么使用树结构
因为线性结构插入和查找不方便、效率不是太高
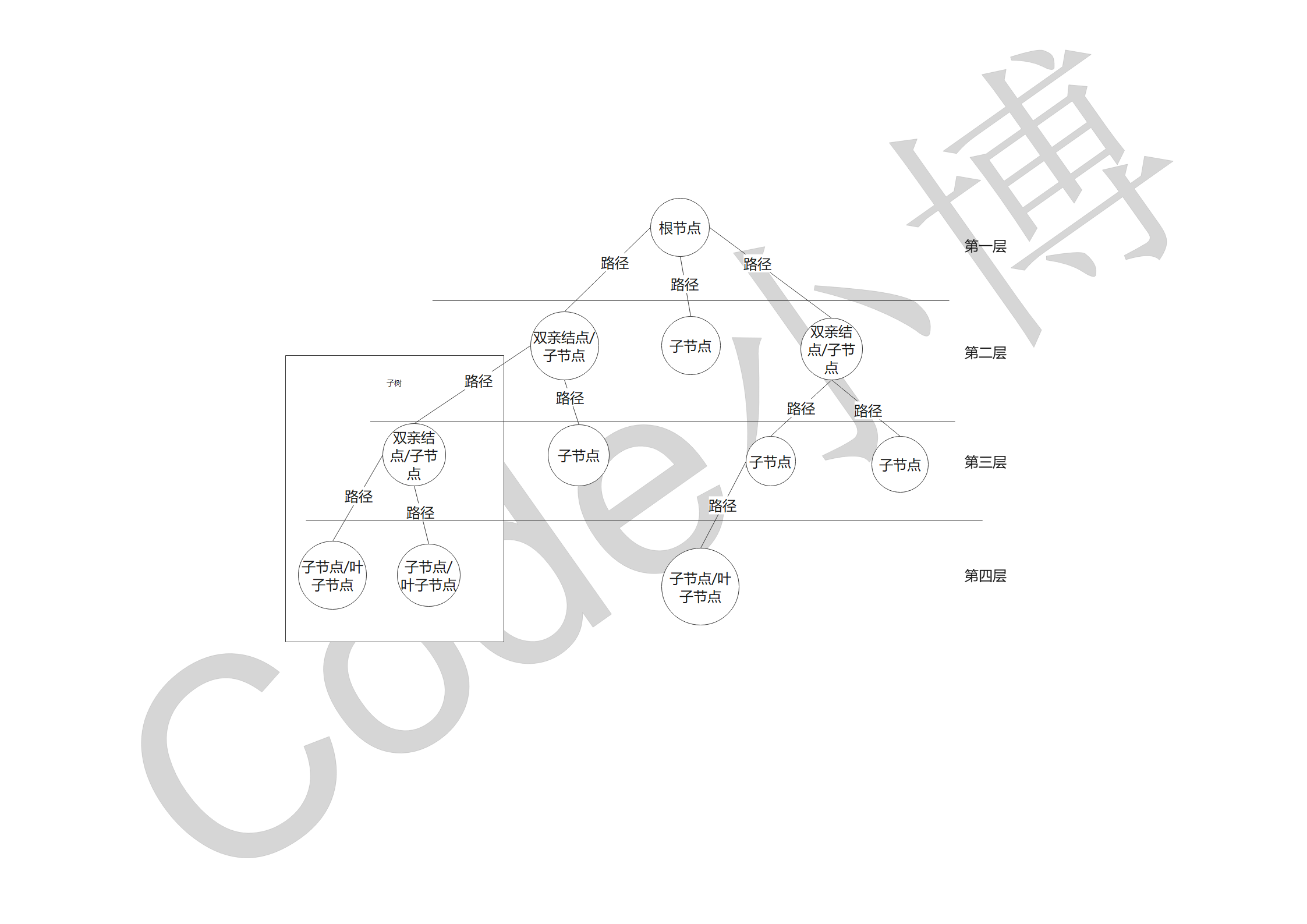
树的基本概念
根节点就是最开始的那一个节点、就是祖宗
双亲节点就是一个节点下面有两个节点、就是他自己即是爹又是娘、自己就能生两个节点出来
子节点就是被生出来的那个
路径就是从一个节点到另一个节点所经过的地方、走的路
节点的度就是一个节点有几个子节点、有几个子节点那么他的度就是多少
节点的权就是当前节点里面存的内容、存的内容是多少它的权就是多少
叶子节点就是当前节点没有子节点、他就是最后一个了
子树就是当前这个树里面的叉、把里面的几个节点也看成一个树、那么这个树就是它的子树
层就是每个节点的层次、就是例如辈分一样、太爷、爷爷、爹、儿子、孙子、重孙子
树的高度就是最大的层数
森林就是将多个树连在一起组成一个森林
二叉树
啥是二叉树
二叉树就是任何一个节点的子节点数量不超过2
二叉树的子节点分为左节点和右节点、并且左右节点不可颠倒位置
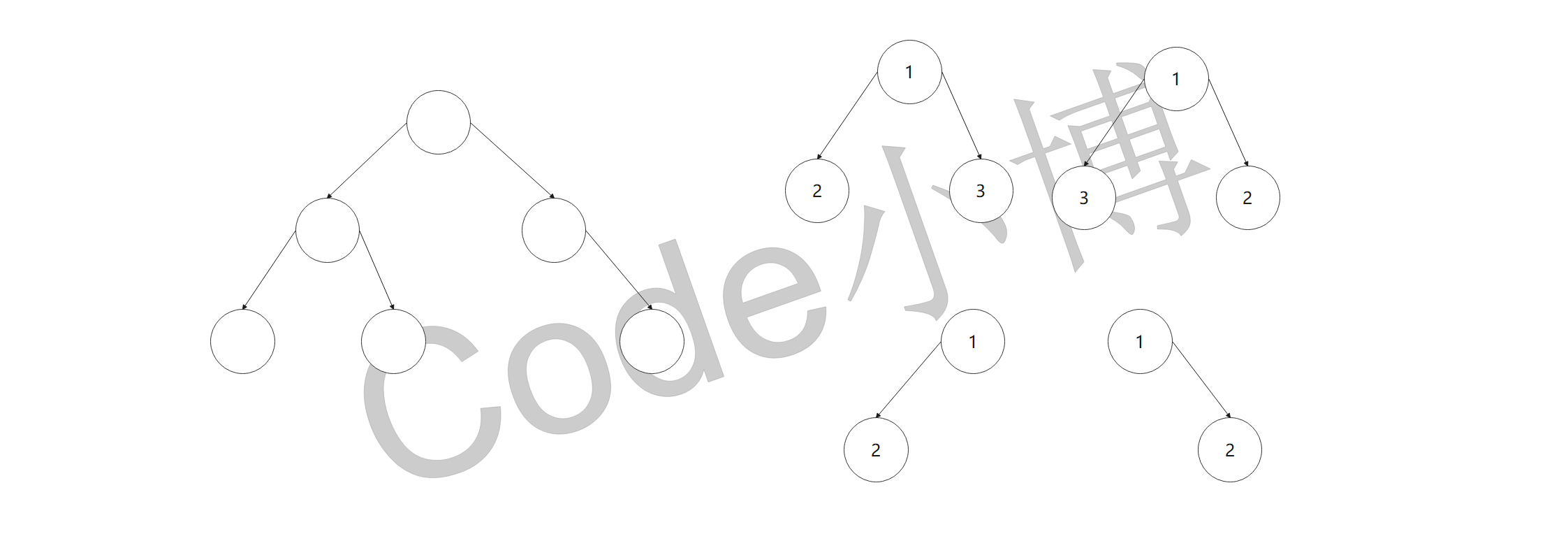
满二叉树
除最后一层无任何子节点外、每一层上的所有结点都有两个子结点的二叉树
一个二叉树、如果每一个层的结点数都达到最大值、则这个二叉树就是满二叉树。也就是说、如果一个二叉树的层数为K、且结点总数是(2^k) -1 则它就是满二叉树
完全二叉树
所有叶子节点都在最后一层或倒数第二层、且最后一层的叶子节点在左边连续、倒数第二层叶子节点在右边连续
一棵深度为k的有n个结点的二叉树、对树中的结点按从上至下、从左到右的顺序进行编号、如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同、则这棵二叉树称为完全二叉树
链式存储的二叉树
CRUD
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
| public class TreeNode {
private Integer value;
private TreeNode leftNode;
private TreeNode rightNode;
public TreeNode(Integer value){
this.value = value;
}
public Integer getValue() {
return value;
}
public void setValue(Integer value) {
this.value = value;
}
public void setLeftNode(TreeNode leftNode) {
this.leftNode = leftNode;
}
public TreeNode getLeftNode() {
return leftNode;
}
public void setRightNode(TreeNode rightNode) {
this.rightNode = rightNode;
}
public TreeNode getRightNode() {
return rightNode;
}
public void frontShow(TreeNode node){
System.out.print(value + "\t");
if(null != leftNode){
leftNode.frontShow(node.getLeftNode());
}
if(null != rightNode){
rightNode.frontShow(node.getRightNode());
}
}
public void middleShow(TreeNode node){
if(null != leftNode){
leftNode.middleShow(node.getLeftNode());
}
System.out.print(value + "\t");
if(null != rightNode){
rightNode.middleShow(node.getRightNode());
}
}
public void rearShow(TreeNode node){
if(null != leftNode){
leftNode.rearShow(node.getLeftNode());
}
if(null != rightNode){
rightNode.rearShow(node.getRightNode());
}
System.out.print(value + "\t");
}
public TreeNode frontSearch(int i){
TreeNode target = null;
if(i == value){
return this;
}
if(null != leftNode){
target = leftNode.frontSearch(i);
}
if(null != target){
return target;
}
if(null != rightNode){
target = rightNode.frontSearch(i);
}
return target;
}
public void delete(int i){
TreeNode node = this;
if(null != leftNode && node.leftNode.value == i ){
node.rightNode = null;
return ;
}
if (null != rightNode && node.rightNode.value == i){
node.rightNode = null;
return ;
}
node = leftNode;
if(node != null){
node.delete(i);
}
node = rightNode;
if(node != null){
node.delete(i);
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| public class BinaryTree {
private TreeNode treeNode;
public TreeNode getTreeNode() {
return treeNode;
}
public void setTreeNode(TreeNode treeNode) {
this.treeNode = treeNode;
}
public void frontShow(TreeNode node){
if(null != treeNode){
treeNode.frontShow(node);
}
}
public void middleShow(TreeNode node){
if(null != treeNode){
treeNode.middleShow(node);
}
}
public void rearShow(TreeNode node){
if(null != treeNode){
treeNode.rearShow(node);
}
}
public TreeNode frontSearch(int i){
return treeNode.frontSearch(i);
}
public void delete(int i){
if(treeNode.getValue() == i){
treeNode = null;
}else{
treeNode.delete(i);
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| public class TestBinaryTree {
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
TreeNode node1 = new TreeNode(1);
TreeNode node2 = new TreeNode(2);
TreeNode node3 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
TreeNode node7 = new TreeNode(7);
tree.setTreeNode(node1);
node1.setLeftNode(node2);
node1.setRightNode(node3);
node2.setLeftNode(node4);
node2.setRightNode(node5);
node3.setLeftNode(node6);
node3.setRightNode(node7);
tree.frontShow(node1);
System.out.println();
tree.middleShow(node1);
System.out.println();
tree.rearShow(node1);
System.out.println();
System.out.println(tree.frontSearch(6));
tree.delete(1);
tree.frontShow(node1);
}
}
|
顺序存储的二叉树
通常情况下只考虑满二叉树和完全二叉树、因为普通的二叉树没有意义
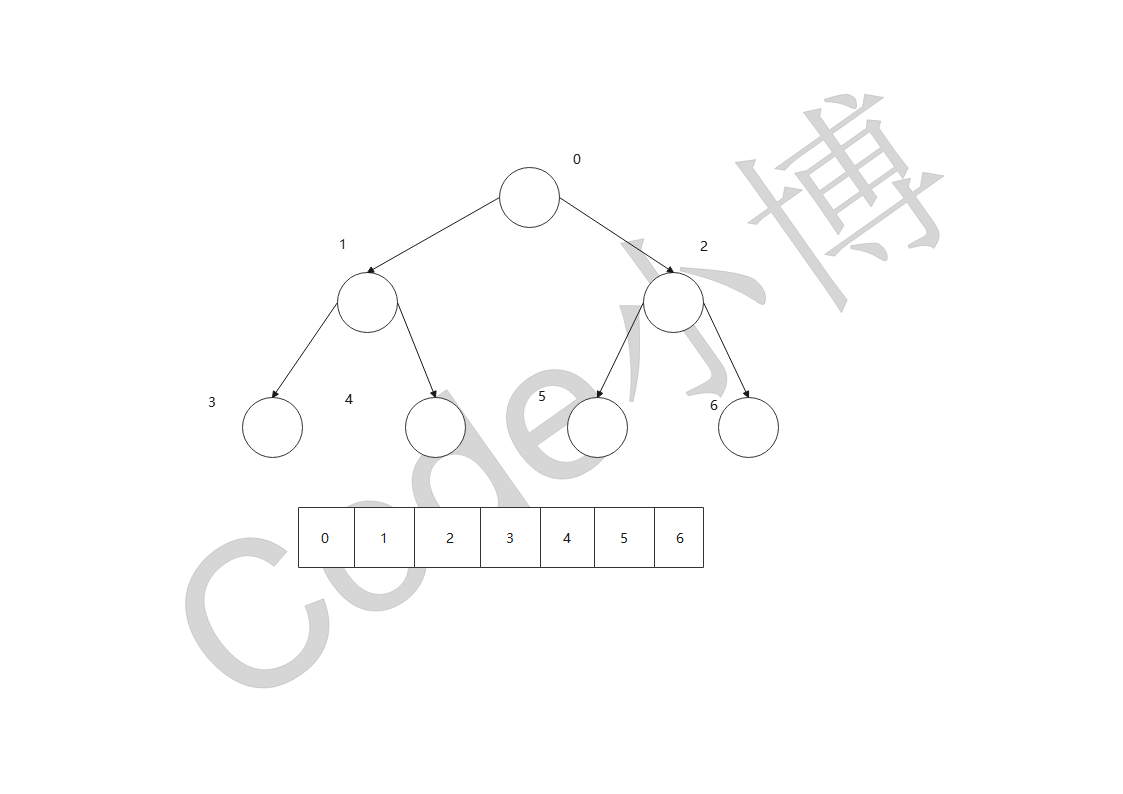
2 * n + 1
2 * n + 2
(n - 1) / 2
顺序存储的二叉树遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| public class ArrayBinaryTree {
private int[] data;
public ArrayBinaryTree(int[] data){
this.data = data;
}
public void frontShow(){
frontShow(0);
}
public void frontShow(int index){
System.out.println(data[index]);
if(data == null || data.length == 0){
return ;
}
if(2 * index + 1 < data.length){
frontShow(2 * index + 1);
}
if(2 * index + 2 < data.length){
frontShow(2 * index + 2);
}
}
}
|
1
2
3
4
5
6
7
8
9
| public class Test {
public static void main(String[] args) {
int[] data = new int[]{1,2,3,4,5,6,7};
ArrayBinaryTree arrayBinaryTree = new ArrayBinaryTree(data);
arrayBinaryTree.frontShow();
}
}
|
正确的开始、微小的长进、然后持续、嘿、我是小博、带你一起看我目之所及的世界……



